

The perimeter of a parallelogram is the total distance enclosed by its boundary. Since the parallelogram is a type of quadrilateral, thus it has four sides. The perimeter of the parallelogram will be equal to the sum of all these four sides. Geometry is a branch of mathematics that deals with the study of different geometrical shapes. It is of two types:
A parallelogram is a two-dimensional geometric shape bounded by four sides. The properties of a parallelogram are:
Now, let us find here the perimeter of parallelogram along with formulas and also see some solved examples to understand better.
The perimeter of a parallelogram is defined as the total length of the boundaries, surrounding it. The sum of all the sides of a parallelogram is known as the perimeter of a parallelogram.
The parallelogram perimeter is similar to the perimeter of the rectangle. Since, both the shapes having similar properties, the area and the perimeter of the parallelogram have more or less the same formulae. By adding all the boundaries or sides of the parallelogram, we can easily find the parallelogram perimeter.
Let “a” and “b” be the sides of a parallelogram. Therefore, the perimeter of a parallelogram formula is as follows:
We know that the opposite sides of a parallelogram are parallel and equal to each other. Thus, the formula for finding the perimeter of a parallelogram is given by:
So, the perimeter of Parallelogram, P = a + b + a + b units
Therefore, the perimeter of a parallelogram, P = 2(a+b) units
We have already discussed the formula to calculate the perimeter of a parallelogram, given the length of its parallel sides. Thus, combining it there are three cases to find the perimeter of a parallelogram, when:
Let us find the perimeter of a parallelogram based on the above three cases.
This is the common scenario, when we have the length of two adjacent sides of a parallelogram given to us. Thus, we can simply the formula:
Perimeter of a parallelogram = 2 (a + b)
where a and b are the length of two adjacent sides of parallelogram
Example: If a = 10 cm and b = 5 cm, then the perimeter of a parallelogram;
P = 2(a + b) = 2(10 + 5) = 2 (15) = 30 cm
The perimeter of the parallelogram with base and height is given using the property of the parallelogram. If “b” is the base of the parallelogram and “h” is the height of the parallelogram, then the formula is given as follows:
According to the property of the parallelogram, the opposite sides are parallel to each other, and the parallelogram perimeter is defined as two times of the base and height.
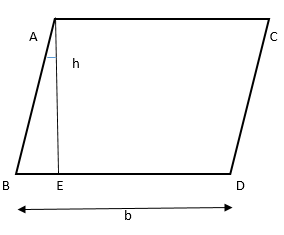
Thus, the formula for the perimeter of a parallelogram is:
where θ is the angle BAE, formed between the height and side of the parallelogram, i.e. AE and AB.
We know that the area of a parallelogram is equal to the product of base and height.
A = b x h square units ……(1)
The relationship between the area and perimeter of a parallelogram is:
Therefore, the value of b in terms of P is
Now, substitute the value of b in (1)
A = ((P/2) – a)h Square units
Find the perimeter of a parallelogram whose base and side lengths are 10cm and 5cm, respectively.
Solution:
Base length of a parallelogram = 10 cm
Side length of a parallelogram = 5 cm
We know that the perimeter of a parallelogram, P = 2(a+b) units.
Substitute the values
Therefore, the perimeter of a parallelogram is 30 cm.
Example 2:
Find the length of another side of the parallelogram whose base is 5 cm and the perimeter is 40 cm.
Solution:
Perimeter, p = 40cm
We know, that the perimeter of a parallelogram is,
Now substitute the given values in the formula,
Thus, the length of other side of the parallelogram is 15 cm.